光线追踪中的辐射度量学
为什么要引入辐射度量学?
在传统的Whitted style ray tracing中,我们的Shading方法本质上还是一个基于经验公式的Phong或者Blinn-Phong光照模型,而并没有真正的基于物理去考虑光以及对应能量应该如何表述。所以为了能够使得Ray Tracer生成高质量图片,我们必须要借助一些成熟的数学物理体系来对光的能量进行描述。辐射度量学(Radiometry)便是一个非常理想的工具。
Radiometry provides a set of ideas and mathematical tools to describe light propagation and reflection. —Pbrtv3 5.4
相关单位定义与解释
首先引入一个最基本的关于辐射能量(Radiant Energy)的定义,我们用符号$Q[J=Joule]$来进行表述,他的单位则是我们自初中物理就非常熟悉的焦耳,不过在计算机图形领域,我们很少直接使用$Q$,因为这个能量很明显是和时间相关的一个量,一个物体接受光照的时间越长,其接受到的能量自然就越高。而在刨除了时间长短这影响后,我们才可以有效的衡量光源强度。而这也就是所谓的Radiant Power或Radiant Flux,数学定义如下。
在有了Radiant Power(后简写为Power)之后,我们便可以轻松的定义Radiant Intensity, Irradiance以及Radiance了。
不过在进行这些物理量的解释之前,我们还需要简单的了解下球面坐标系。
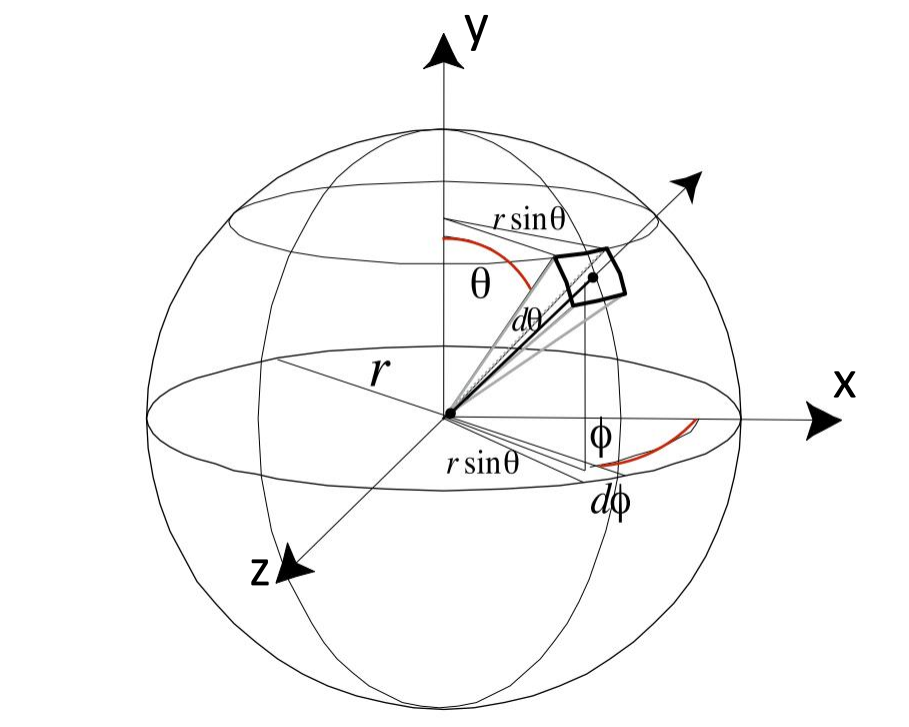
球面坐标系上的坐标是通过一个三元组$(r,\theta,\phi)$来确定,其中$r$代表到原点的距离,$\theta$代表与$y$轴的夹角,$\phi$代表与$x$轴的夹角。其与笛卡尔坐标系的转换其实也非常简单,公式如下:
使用球面坐标系的好处主要是方便我们更好的对光线进行建模,因为可以看到在球面坐标系中,我们更多的是基于角度(方向)而不是坐标值来进行考虑,这对于之后的理解毫无疑问是大有脾益的。
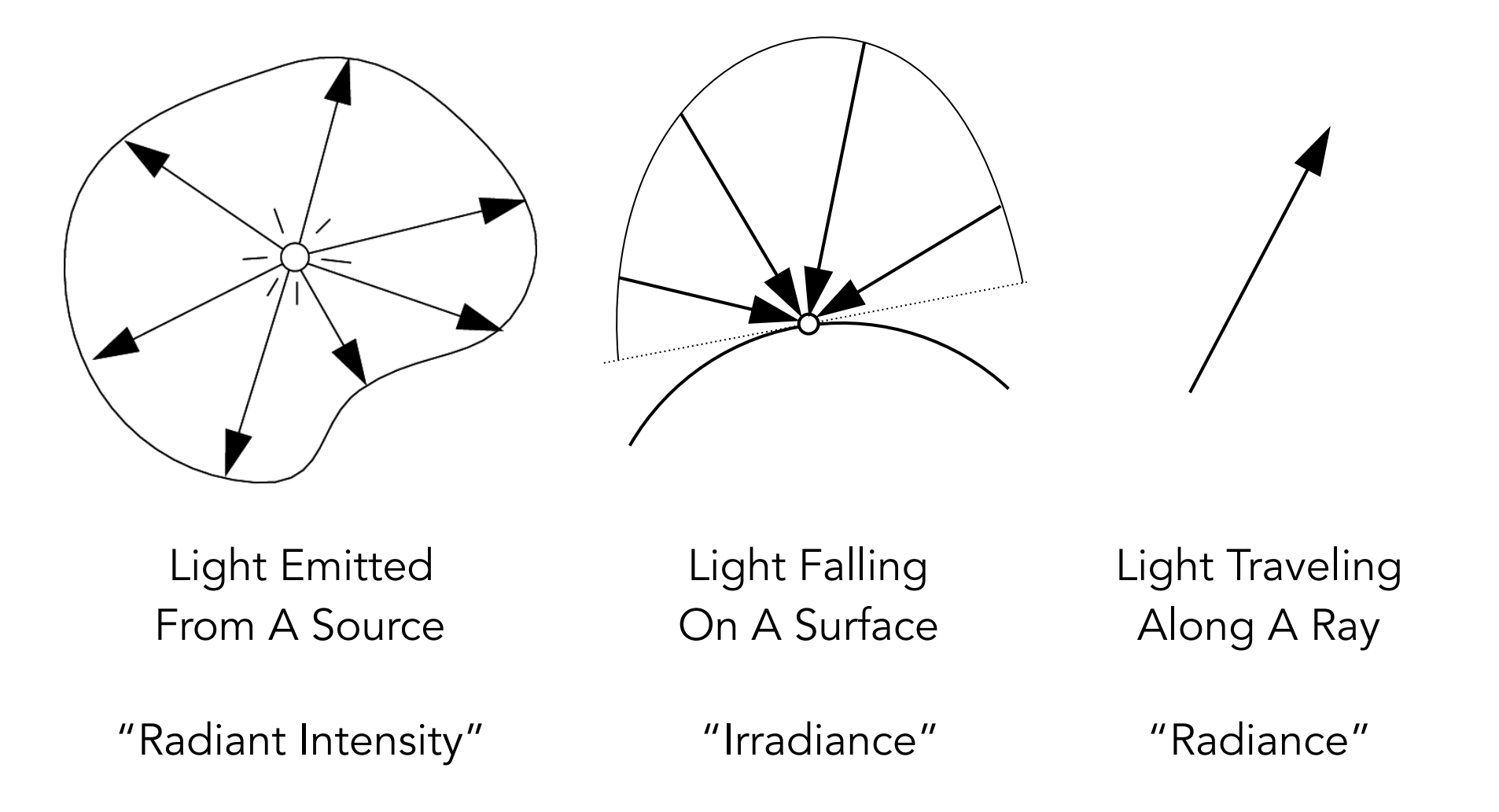
Radiant Intensity
Radiant Instensity,从官方的定义来讲是Power per unit solid Angle,也就是在每个单位立体角方向上中所释放的功率。
立体角的定义其实可以类比弧度制中弧度的定义,其定义为球面上延申面积与半径平方的比值。

Irradiance和Radiance
Irradiance则是定义为power per project area, 即
这里$dA$代表的是面积,可以看到与Radiant Intensity的不同就是在于Intensity是定义在立体角上,而Irradiance是定义在面积之上。
Radiance则可以是认为在Irradiance上进一步考虑每个立体角的贡献。也就是所谓的power per area per solid angle, 从数学上则定义为
这里的$\theta$代表平面法线与当前立体角方向的夹角。
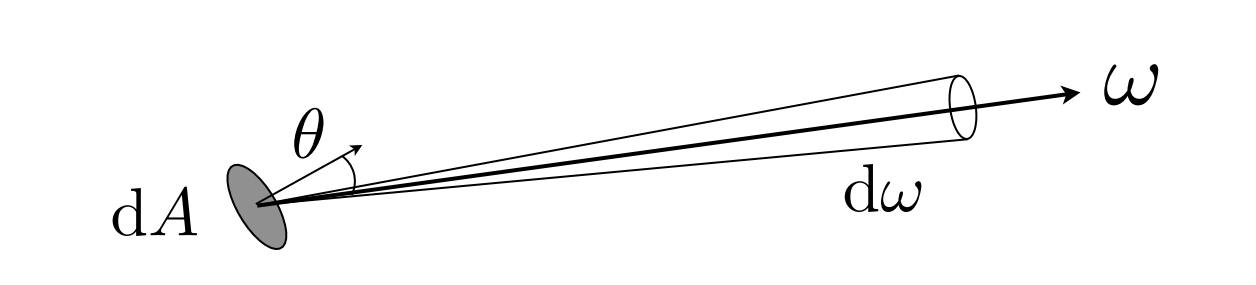
简单的看过来的话,Irradiance和Radiance的差别其实就是在于方向性,Radiance本质上可以看作Irradiance per unit solid angle。
总结
总的来看,图形中的辐射度量学关键在于理解Irradiance和Radiance,这是构建PathTracer和渲染方程的基础,也是理解如何定量分析光照能量的关键。基于物理的渲染,一个最基本的要求便是能量守恒,所以说引入辐射度量学这套分析工具是十分有必要的。