弹簧质点系统(Mass-Spring System)

弹簧质点系统算是最简单的一种物理模型，它假设所有物体除了质点，便是连接质点的弹簧。在这种情况下，我们需要分析的力非常简单，基本上只用考虑重力以及弹簧力即可。公式则如下图所示。

代码地址: https://github.com/WeebOwO/MassSpringSystem

具体实现

整体的结构如下面的伪代码所示，我们在主循环里面首先处理一下各种事件，然后物理引擎往前步进一段时间，最后提交给渲染器进行渲染。

1
2
3
4
5
# main loop
while True:
    process_event()
    engine.step()
    render()

而具体到这个engine.step()函数，我们所做的事情则是计算每个点的受力，并根据受力计算出对应的速度，加速度，以及对应的位移。

1
2
3
4
# engine.step()
def step():
    calclate_force() # 计算力
    solve() # 在这里求解各种各样的速度，并根据自定义delta time进行迭代

从更为专业的术语上解释的话，我们其实是在各个离散的时间步长上进行物理量的累加，从而模拟连续世界中的积分。因为在实际物理世界中有加速度的存在，物体每个时间的速度都不相同，我们应该根据速度在时间的积分来得到真正的位移，但是计算机是无法做到所谓的“连续”的，所以我们进而采用了在每个细小时间步长上进行累加的做法。而这种模拟方法其实也有各种各样的流派，我们所使用的是较为简单的欧拉方法。

欧拉方法主要有三种流派

  1. 显式欧拉方法（explicit Euler method）

  1. 半隐式欧拉方法（semi-implicit Euler method）：

  1. 隐式欧拉方法（implicit Euler method） ：

我们在这里所使用的是半隐式欧拉方法（semi-implicit Euler method）来进行模拟，代码可以描述为如下。

1
2
3
4
5
6
7
8
9
# calclate_force
for i in range(particle_num):
            self.particle_force[i] = ti.Vector([0.0, -gravity]) * self.particle_mass
            for j in range(particle_num):
                if self.rest_length[i, j] != 0:
                    # spring force i 
                    vec_ij = self.particle_pos[i] - self.particle_pos[j]
                    direction = vec_ij.normalized()
                    self.particle_force[i] += -self.young_modulus[None] * (vec_ij.norm() / self.rest_length[i, j] - 1) * direction
1
2
3
4
5
6
7
8
# sovle
for i in range(particle_num):
            if not self.particle_fixed[i]:
                self.particle_velocity[i] += self.delta_time * self.particle_force[i] / self.particle_mass
                self.particle_velocity[i] *= ti.exp(-self.delta_time)
                self.particle_pos[i] += self.particle_velocity[i] *self.delta_time
            else:
                self.particle_velocity[i] = ti.Vector([0.0, 0.0])

在计算力的阶段，我们首先把当前所有的质点的力都假设为只有重力，然后再遍历其他的质点，如果发现两个质点有弹簧，那么我们就计算下当前质点所受到的弹簧力。而求解的话则是按照我们之前所讲的根据力来进行加速度，速度，以及位移的迭代。

最后的运行的效果如下图所示(可能加载的会有些慢，大概是1m左右的gif图)

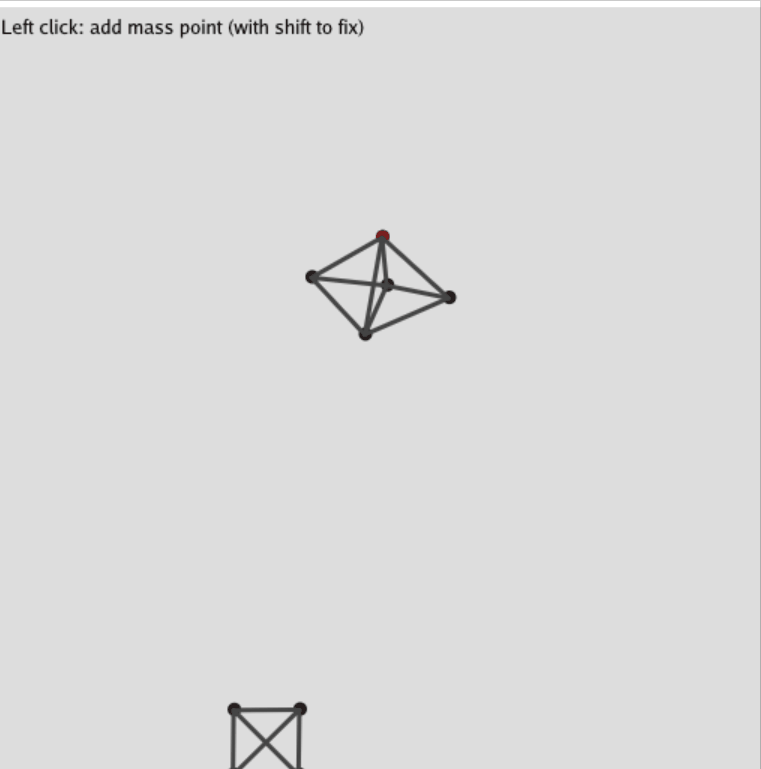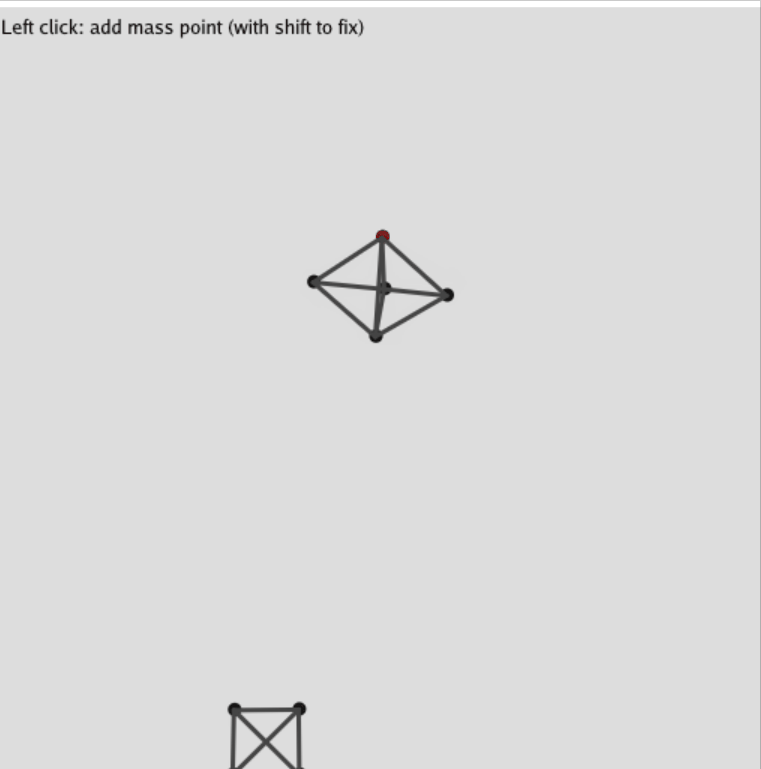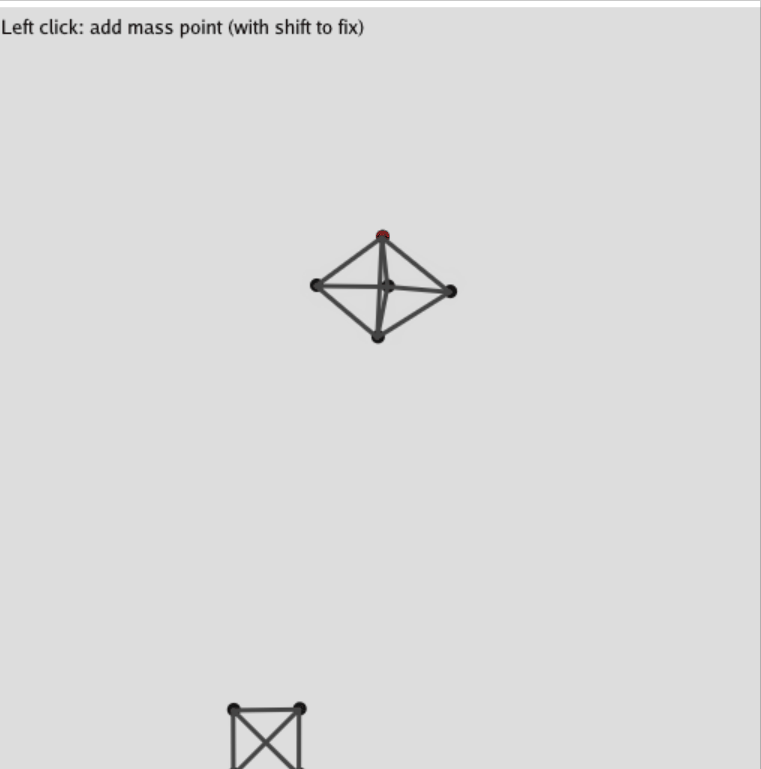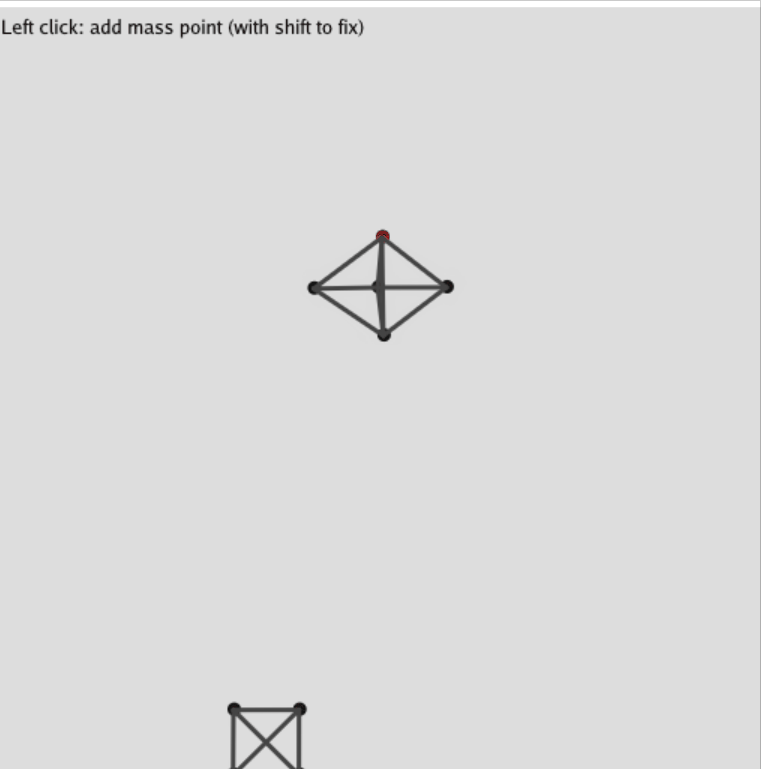
总结

弹簧质点系统本身的实现并不困难，但是看起来还是蛮有意思的，并且也能学习到物理引擎大体上是怎么个流程，也算是有点收获吧。